Aaryamann Challani

Engineer and amateur cook writing about privacy, cryptography, and distributed systems

← Back to posts
May 03, 2021

Introduction

Zero knowledge proofs are cryptographical methods by which one can prove to another that they know a certain value “z” without conveying the actual value “z” to the other person. Understanding them will be easier with the help of an example —

  • Alice is color-blind and Bob isn’t

  • Alice has two balls, one green and one red. She is unable to tell the difference between the two.

  • Alice does not believe that Bob is not color blind

  • To verify his claim, Alice holds both balls in her hands and tells Bob that she will either switch/not switch them behind her back, but Bob must tell her if she has switched the balls. If Bob is not color blind, he will be able to tell whether she has switched the balls.

  • In the first try of Bob guessing if the ball has switched, he has a 50% chance of guessing it right. Hence, Alice conducts the experiment 20 times in a row. The probability that Bob guessed all of them are right is 9.53674316e^-7. Which is sufficiently small to assume that Bob is, in fact, not colorblind.

  • This way, one can confirm the knowledge of the prover without the verifier knowing anything about it.

History

  1. Zero Knowledge Proofs were conceived by 1985 by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in their paper “The Knowledge Complexity of Interactive Proof-Systems”.

  2. Goldwasser, Micali and Rackoff wrote mainly about Interactive Proofs(IP)

  3. In 1988, Non-Interactive Zero Knowledge Proofs were conceived by Blum, Feldman, and Micali. They are also known as zk-SNARKs/zk-STARKs.

  4. A common reference string shared between the prover and the verifier is sufficient to achieve computational zero-knowledge without requiring interaction. Goldreich and Oren gave impossibility results for one shot zero-knowledge protocols in the standard model. In 2003, Goldwasser and Kalai published an instance of an identification scheme for which any hash function will yield an insecure digital signature scheme.

  5. The first widespread application of zk-SNARKs was in the Zerocash blockchain protocol, where zero-knowledge cryptography provides the computational backbone.

  6. It is assumed that By this year, 82 cryptocurrencies worth a total of US$8.85 billion encrypted their transactions with zero-knowledge proofs or a similar private technology.

Precursory Information

To understand the math behind it, one must have knowledge of Elliptic Curve Cryptography, or ECC in short.

An elliptic curve is the set of points that satisfy a specific mathematical equation. The equation for an elliptic curve looks something like this:

Example Equation

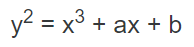
ECC Visualization

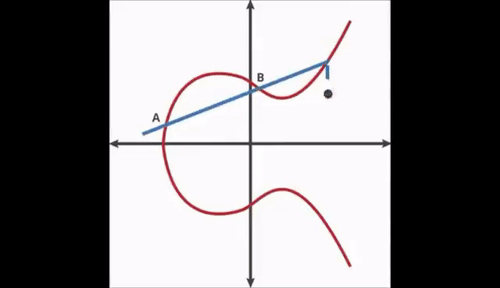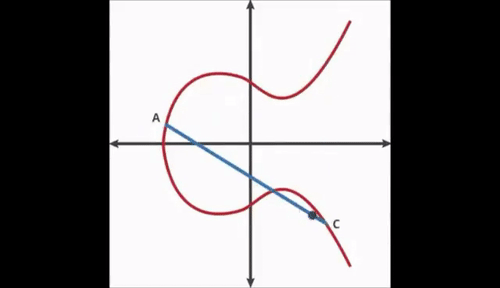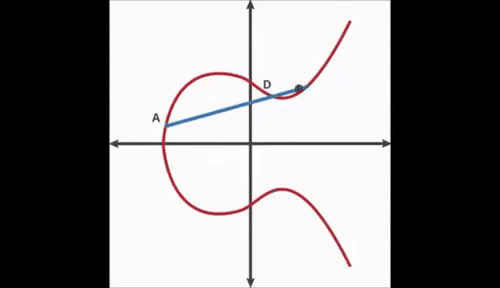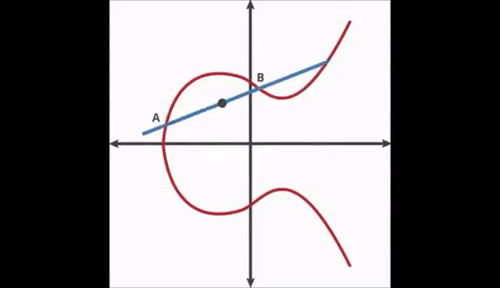
Elliptic Curves have symmetry about the x axis, and any non-vertical line will intersect the curve in at most three places.

First, we start with an arbitrary point on the curve. Next, we use the dot function to find a new point. We keep repeating the dot function recursively.

If you do this 3 times you may notice that you end at a point E. If you know the starting point, ending point and number of hops it is easy to land at that point. However, if you have no knowledge of the number of hops, it is nearly impossible to arrive at the ending point.

Practically, ECC relies on the existence of a private key and a public key. The private key is used to encrypt the data into a hash, and that hash can be used to verify the owner.

Think of the public key as the starting point and ending point, and the private key as the number of hops.

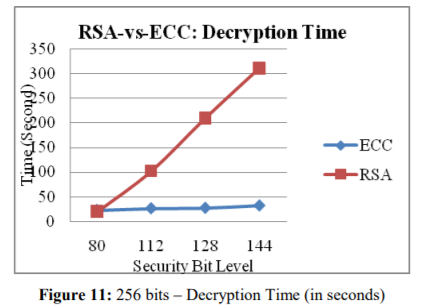
ECC is important because it provides the same level of encryption as RSA, but with a much reduced bit count.

Comparison between RSA and ECC decryption time

Quadratic Residue: In number theory, an integer q is called a quadratic residue modulo n if it is congruent to a perfect square modulo n; i.e., if there exists an integer x such that:

Quadratic Residue

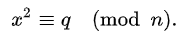
A great explanation for quadratic residues is provided by Polar Pi.

The Math

zk-Proofs and IoT

Internet of Things (IoT) devices are being deployed in huge numbers around the world, and often present serious vulnerabilities. Accordingly, delivering regular software updates is critical to secure IoT devices.

Manufactures face two predominant challenges in providing software updates to IoT devices:

  1. scalability of the current client-server model and

  2. integrity of the distributed updates — exacerbated due to the devices’ computing power and lightweight cryptographic primitives

Crowdpatching, is a protocol leveraging zk-proofs and Blockchains to deliver security patches to IoT devices.

In this system, the manufacturer delegates the delivery of new updates to self-interested agents, called distributors, who undertake this task in exchange for cryptocurrency (CC) payments.

In this context, the use of a zero-knowledge tool, called zk-SNARKs, is fundamentally important.

Before a proof-of-delivery can be issued, a distributor is expected to provide a zk-SNARKs proof about the provided encrypted update, mathematically proving that: 1) it was indeed obtained encrypting the update file authorized by the manufacturer and 2) the employed key has indeed the provided hash value.

Most importantly, this zero-knowledge proof does not reveal anything else beyond those facts: the unencrypted update and the key remain secret.

If the proof is valid, then the proof-of-delivery signature is generated by the IoT device, and sent to the Smart Contract by the distributor along with the encryption key.

Before issuing the payment, the contract checks that the signature is valid, and that the key matches the hash value. Along with the payment, the SC publishes the key on the BC. The latter can be now used to decrypt the file, and the update is finally obtained by the IoT device.

This was one example of many, on how the strong cryptography protocol of zk-SNARK’s can secure IoT devices.

Limitations of zk-Proofs

  • The computational power required to generate a proof is significantly higher than other protocols.

  • The space taken up by said proofs are significantly higher than other protocols as well.

  • If the prover loses access to the secret, it is lost forever (this could be an advantage in some cases)

Current Applications

  • Zero Knowledge Proofs are used widely in truly private cryptocurrency transactions, as seen on the prominent L2 solution, ZK-Rollups

  • Crowdpatching

  • Highly secure authentication systems

  • Securing Intellectual Property

References